Projects

Below are some projects that we are currently working on / or have worked on in the past.

Deep Learning and Graph Isomorphism

Graph isomorphism is a fundamental concept for exploiting the structure of graphs. This project aims to develop new heuristic techniques and theories for graph isomorphism, advancing state-of-the-art methodologies for its applications in solving real-world problems. Inspired by recent advances in machine learning, this project will investigate graph isomorphism problems from a deep learning perspective by marrying the best approaches from classic graph isomorphism studies with new techniques from modern AI. This is an important step towards bridging the gap between combinatorical generalization and deep learning.

(This research is funded by the Australian Government through the Australian Research Council.)

List of recent publications

  • A New Perspective on “How Graph Neural Networks Go Beyond Weisfeiler-Lehman?”, A. Wijesinghe and Q. Wang, International Conference on Learning Representations (ICLR - Oral, 54 out of 3391 submissions) 2022 ( preprint | oral video | poster video | code )

  • N-WL: A New Hierarchy of Expressivity for Graph Neural Networks”, Q. Wang, D. Chen, A. Wijesinghe, S. Li, and M. Farhan, International Conference on Learning Representations (ICLR) 2023 ( pdf | slides | poster | code )

  • Local Vertex Colouring Graph Neural Networks, S. Li, D. Kim, and Q. Wang, 40th International Conference on Machine Learning (ICML), 2023 ( pdf | poster | code )

  • Contrastive Learning for Supervised Graph Matching, G. Ratnayaka, Q. Wang, and Y. Li, 39th Conference on Uncertainty in Artificial Intelligence (UAI), 2023 ( pdf | poster | code )

Geometric Graph Learning

Geometric graph learning is an emerging field of machine learning, which aims to apply deep learning techniques to learn from complex data like graphs. In recent years, Graph Neural Networks (GNNs) as a powerful deep learning approach have been widely applied in various fields. However, graphs are in irregular non-Euclidean domains. This brings up the challenge of how to design deep learning techniques in order to effectively extract useful features from arbitrary graphs. In this project, we aim to explore the mathematical foundations of graph learning techniques and develop neural networks for graphs in a principled way.

List of recent publications

  • DFNets: Spectral CNNs for Graphs with Feedback-Looped Filters, A. Wijesinghe and Q. Wang, The 33rd Conference on Neural Information Processing Systems (NeurIPS), 2019 ( pdf | arXiv | slides | poster | code )

  • Beyond Low-Pass Filters: Adaptive Feature Propagation on Graphs, S. Li, D. Kim, and Q. Wang, The European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML-PKDD), 2021 ( pdf | arXiv | code )

  • A Regularized Wasserstein Framework for Graph Kernels, A. Wijesinghe, Q. Wang and S. Gould, IEEE International Conference on Data Mining (ICDM), 2021 ( pdf | arXiv | code )

  • Restructuring Graphs for Higher Homophily via Adaptive Spectral Clustering, S. Li, D. Kim, and Q. Wang, Thirty-Seventh AAAI Conference on Artificial Intelligence (AAAI - Oral), 2023 ( pdf | arXiv | poster | code )

  • Geometric Learning on Graph Structured Data, A. Wijesinghe, PhD thesis, Australian National University, 2023 ( pdf )

Shortest-Path Algorithms

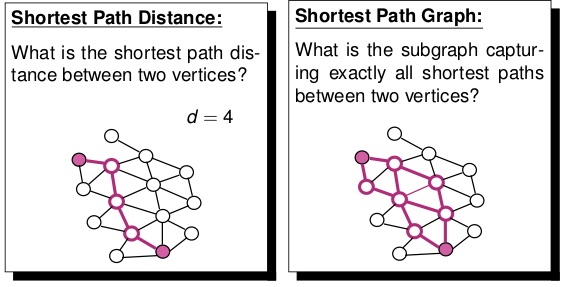Finding the shortest-path information (e.g., distance, paths, counting of paths) between a pair of vertices is a fundamental task in graph theory. Despite efforts for many years, there is still a high demand for scalable solutions over large and ever-growing networks. Questions of interest include: (1). How to develop robust, efficient and scalable solutions for shortest-path related problems on large networks with possibly billions of vertices? (2). How to handle dynamics of networks, i.e., topological structure changes caused by node and edge insertions and deletions? (3). What kinds of the theoretical properties can we gurantee in our soltions?

List of recent publications

  • A Highly Scalable Labelling Approach for Exact Distance Queries in Complex Networks, M. Farhan, Q. Wang, Y. Lin, and B. Mckay, The 22nd International Conference on Extending Database Technology (EDBT), 2019 ( pdf | arXiv | slides | code )

  • Efficient Maintenance of Distance Labelling for Incremental Updates in Large Dynamic Graphs, M. Farhan and Q. Wang, The 24th International Conference on Extending Database Technology (EDBT), 2021 ( pdf | arXiv | slides | poster | video | code )

  • Query-by-Sketch: Scaling Shortest Path Graph Queries on Very Large Networks, Y. Wang, Q. Wang, H. Koehler, and Y. Lin, ACM SIGMOD International Conference on Management of Data (SIGMOD), 2021 ( pdf | arXiv | slides | video | code )

  • Exploring Shortest Paths on Large-scale networks, Y. Wang, MPhil thesis, Australian National University, 2021 ( pdf )

  • Fast Fully Dynamic Labelling For Distance Queries, M. Farhan, Q. Wang, Y. Lin, and B. Mckay, The VLDB Journal, 2021 ( pdf | code )

  • BatchHL: Answering Distance Queries on Batch-Dynamic Networks at Scale, M. Farhan, Q. Wang, and H. Koehler, ACM SIGMOD International Conference on Management of Data (SIGMOD), 2022 ( pdf | arXiv | slides | video | code )

  • Answering Shortest Path Distance Queries in Large Complex Networks, M. Farhan, PhD thesis, Australian National University, 2022 ( pdf )

  • Efficient Maintenance of Highway Cover Labelling for Distance Queries on Large Dynamic Graphs, M. Farhan and Q. Wang, World Wide Web, 2023 ( pdf | code )

  • BatchHL+: Batch Dynamic Labelling for Distance Queries on Large-Scale Networks, M. Farhan, H. Koehler, and Q. Wang, The VLDB Journal, 2023 ( pdf | code )

  • Hierarchical Cut Labelling - Scaling Up Distance Queries on Road Networks, M. Farhan, H. Koehler, R. Ohms, and Q. Wang, ACM SIGMOD International Conference on Management of Data (SIGMOD), 2024 ( pdf | arXiv | code )

Deep Learning for Knowledge Tracing

Knowledge tracing is an important task in a wide range of applications in education, such as massive open online courses (MOOCs), intelligent tutoring systems, educational games, and learning management systems. It models dynamics in a student’s knowledge states in relation to different learning concepts through their interactions with learning activities. The goal of the project is to develop machine learning technqiues for capturing knowledge states dynamically and discovering their dependencies on latent learning concepts through the analysis of students’ learning behaviors.

(This research was partially funded by an ANU Vice-Chancellor’s Teaching Enhancement Grant.)

List of recent publications

  • Knowledge Tracing with Sequential Key-Value Memory Networks, G. Abdelrahman and Q. Wang, ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), 2019 ( pdf | slides )

  • Deep Graph Memory Networks for Forgetting-Robust Knowledge Tracing, G. Abdelrahman and Q. Wang, IEEE Transactions on Knowledge and Data Engineering (TKDE), 2022 ( pdf | arXiv )

  • Knowledge Tracing: A Survey, G. Abdelrahman, Q. Wang, and B. Pereira Nunes, ACM Computing Surveys, 2022 ( pdf | arXiv )

  • Learning Data Teaching Strategies Via Knowledge Tracing, G. Abdelrahman and Q. Wang, Knowledge-Based Systems, 2023 ( pdf | arXiv )

  • DBE-KT22: A Knowledge Tracing Dataset Based on Online Student Evaluation, G. Abdelrahman, S. Abdelfattah, Q. Wang, and Y. Lin, 2022 ( arXiv )

  • Knowledge Tracing Using Deep Learning Methods, G. Abdelrahman, PhD thesis, Australian National University, 2023 ( pdf )

Differential Privacy on Graphs

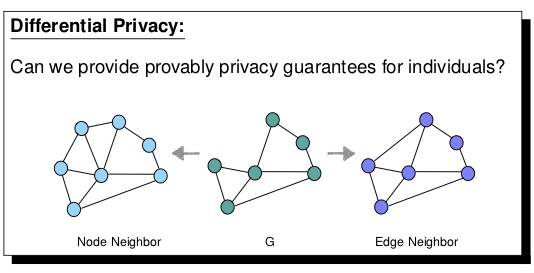Differential privacy (DP) has received increasing interests in recent years. It offers a robust privacy guarantee while making no assumptions about the prior knowledge of an adversary. Although appealing, it is acknowledged that designing differentially private data publishing mechanisms is challenging, particularly on graph-structured data which is often highly sensitive to structural changes. This project aims to develop algorithms and techniques that enable to publish graph-structured data under differential privacy (including edge DP and node DP) while preserving data utility as much as possible.

List of recent publications

  • Publishing Differentially Private Datasets via Stable Microaggregation, M. Iftikhar, Q. Wang, and Y. Lin, The 22nd International Conference on Extending Database Technology (EDBT), 2019 ( pdf | poster )

  • dK-Microaggregation: Anonymizing Graphs with Differential Privacy Guarantees, M. Iftikhar, Q. Wang, and Y. Lin, The 24th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), 2020 ( pdf | slides | video )

  • dK-Projection: Publishing Graph Joint Degree Distribution with Node Differential Privacy, M. Iftikhar and Q. Wang, The 25th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), 2021 ( pdf | slides | video )

  • dK-Personalization: Publishing Network Statistics with Personalized Differential Privacy, M. Iftikhar, Q. Wang, and Y. Li, The 26th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), 2022 ( pdf | slides )

  • Privacy-Preserving Data Publishing, M. Iftikhar, PhD thesis, Australian National University, 2022 ( pdf )

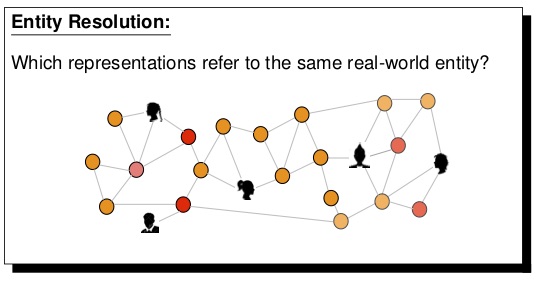Entity Resolution with Active Learning

Entity Resolution (ER) is an important and ubiquitous component of real-world applications in various fields, such as national census, health sector, and crime and fraud detection. A major challenge in learning-based entity resolution is how to reduce the label cost for training. Due to the quadratic nature of record pair comparison, labeling is a costly task that requires a significant effort from human experts. This challenge is further aggravated when the underlying data distribution is highly imbalanced, which commonly occurs in entity resolution applications. The project aims to investigate active learning techniques for entity resolution.

(This research was partially funded by the Australian Government through the Australian Research Council.)

List of recent publications

  • Active Blocking Scheme Learning for Entity Resolution, J. Shao and Q. Wang, The 22nd Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), 2018 ( pdf )

  • Repairing of Record Linkage: Turing Errors into Insight, Q. Bui-Nguyen, Q. Wang, J. Shao, and D. Vatsalan, The 22nd International Conference on Extending Database Technology (EDBT), 2019 ( pdf )

  • Skyblocking for Entity Resolution, J. Shao, Q. Wang and Y. Lin, Information Systems, Volume 85, November 2019 ( pdf | arXiv )

  • Learning to Sample: an Active Learning Framework, J. Shao, Q. Wang and F. Liu, IEEE International Conference on Data Mining (ICDM), 2019 ( pdf | arXiv )

  • ErGAN: Generative Adversarial Networks for Entity Resolution, J. Shao, Q. Wang, A. Wijesinghe, and E. Rahm, IEEE International Conference on Data Mining (ICDM), 2020 ( pdf | arXiv )

  • Entity Resolution with Active Learning, J. Shao, PhD thesis, Australian National University, 2021 ( pdf )